在很多时候，实验所采集到的信号都是包含各种噪声的，在对信号进行进一步分析之前，如何将有效的信号提取出来，是信号与系统领域一个比较热门的话题。

信号的构成

一般将采集到的信号认为是一个有效信号加上一个噪声构成。
假设采集到长度为n的带噪声信号$y_n$,有效信号为$f_n$,噪声信号为$e_n$

那么，采集到的信号就可以表示为$y_n = f_n + e_n$

而噪声信号一般认为是高斯白噪声信号，因为设备自带的伪噪声干扰都是确切的，可以通过特定方式有效去除。噪声信号服从正态分布$N(0,\delta^2)$。

一般用信噪比(SNR)来表示信号的噪声强度。对于归一化信号(即有效信号的极大值为1)，信噪比有

$SNR = 1/\beta^2$

其中$\beta^2$为无信号区域（即有效信号强度为0的区域）的纯噪声信号的标准差。

直接对多个信号进行叠加

因为不同的高斯噪声$e_n$之间相关性为0，且高斯噪声的均值为0，而有效信号在特定点的值不变。所以将多个采集信号相叠加，将会使得有效信号强度不断增加，而噪声信号会不断趋近于0。

根据中心极限法则，相较于原始数据，将n个不同的采集信号叠加后，信噪比将会提高$\sqrt{n}$倍。所以这个方法的缺点也特别明显，如果需要将信噪比提升10倍，那么就至少需要采集100个数据才能达到这个效果，但是往往由于条件的限制，或者单次采样的耗费时间过长，没有办法采集到足够多的数据。

这个方法的优点也非常明显，就是只要单纯提高数量就可以获得非常准确的有效数据，不会引入其他的数据。

基于统计学中重采样原理的数据后处理方法(NASR)

由于采集信号中的高斯噪声具有随机性，假如对采集信号进行随机重采样，那么有效信号在频域中将会呈现出一定的稳定性，峰值变化较小，而噪声信号在频域中的位置会呈现不确定性，峰值剧烈变化。根据这个原理，对采集信号进行重采样之后计算各个点位的相对标准偏差(RSD)值，再通过一个权重矩阵

$w = \alpha + \frac{1- \alpha}{1+e^{\beta*(RSD-\epsilon)}}$

当然也可以使用别的权重矩阵，但是这个权重矩阵是比较好用的。

实现过程

注：在进行NASR之前，需要将信号中的强峰去除，以免在重采样过程中引入较强的伪峰。

• 1.对信号进行快速傅里叶变换(FFT)
• 2.选取合适的阈值，将strong_peak频率剪除
• 3.将反变换数据进行重采样，随机抽取50-65%数据，其他数据设置为0，共采样m次
• 4.计算m个数据集中各个点位的标准差STD以及均值MEAN。标准偏差RSD = STD/MEAN
• 5.将RSD带入权重矩阵中，就可以得到各个点位的信号概率

去噪效果

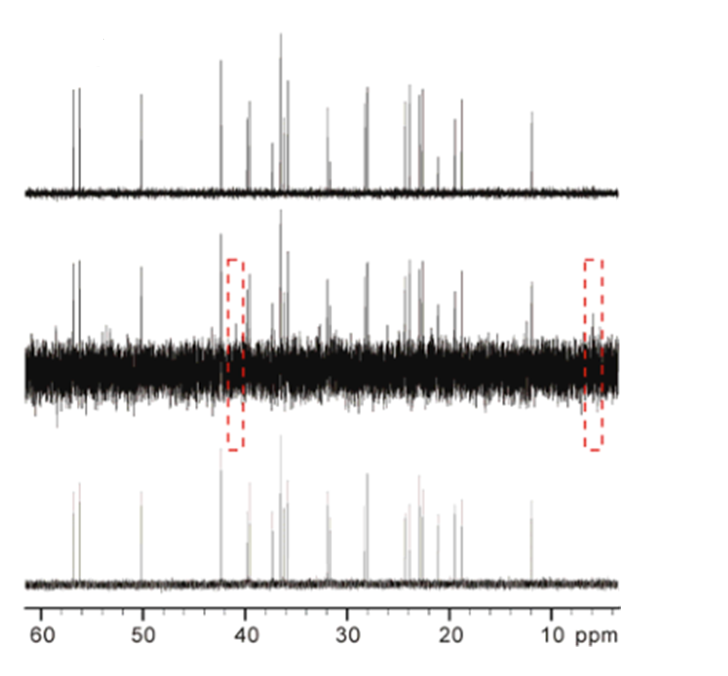
最上方为NASR去噪谱图，中间是噪声谱，下面是参考谱图
可以看到，红色框内的噪声信号为较强的伪峰，NASR可以有效的去除伪峰。
但是NASR的缺点也很明显，引入的参数数量过多，有非常强的主观臆断。而且波峰的失真也比较严重。

Hankel矩阵奇异值分解去噪(HSVD)

可以知道，有效信号的值一般都具有低秩性，即有效信号张成的矩阵一般存在秩亏，rank( $f_n$ ) < r,而随机高斯噪声一般是满秩的。所以如果将采集信号矩阵进行正交分解，并且使高秩部分为0，那么就可以在一定程度上去除噪声信号。

而对矩阵进行正交分解，一般使用奇异值分解(SVD)办法

$F_n = USV$
S是一个对角矩阵，也叫SVD的特征矩阵，而U和V是一对共轭转置的正交矩阵，满足$U*U^T = I$。

将一维信号张成矩阵的办法有很多，但要求构建的矩阵具有低秩性，一般会选用Hankel矩阵，或者Toeplitz矩阵。

Hankel是指每一条逆对角线上的元素都相等的矩阵。

Toeplitz矩阵的主对角线上的元素相等，平行于主对角线的线上的元素也相等

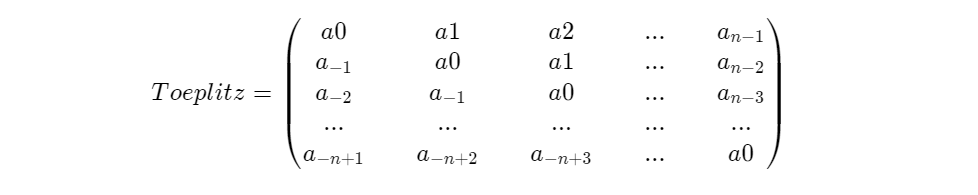
实现过程

• 构造Hankel矩阵。将信号拆成两个部分，其中一部分构成Hankel矩阵的第一行，另一部分构成第一列。一般选择对半分，最中间的值重叠，如N=4096的数据拆成[0:2048]和[2047:4096]两个部分。
• 对大小为M * N的Hankel矩阵进行SVD分解，得到USV三个矩阵。其中S矩阵为M * M的幺正矩阵。
• 根据特征矩阵S的大小，截取对角线值的能量的90%位置，截取后的大小为M * K。
• 使用SVD投影法合成去噪矩阵$H_K$ ,($H_k = S * S_K^H * H$)
• 因为$H_k$不再具有Hankel矩阵的特性，所以需要将反对角线的值取平均来得到去噪的信号。

去噪效果

去噪谱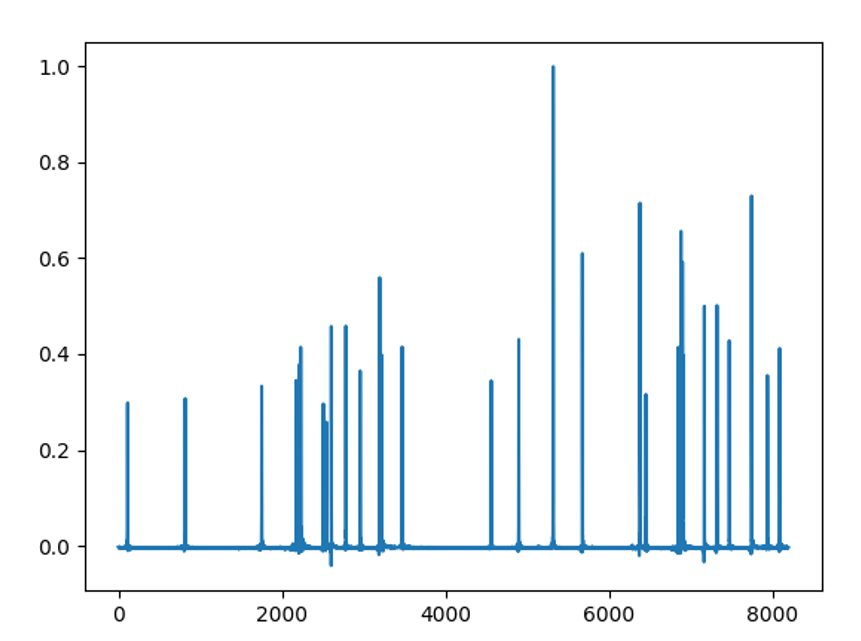

噪声谱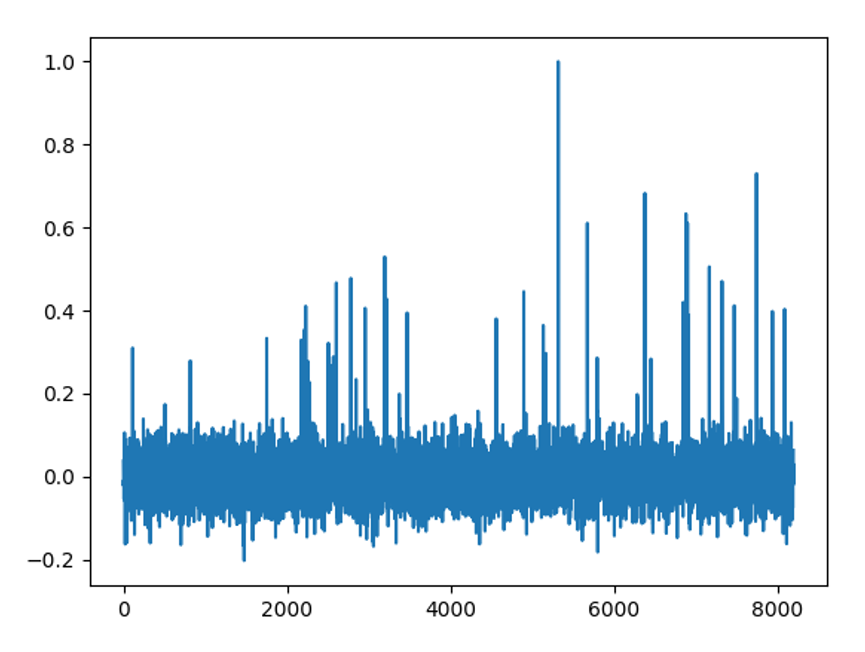

可以看到，去噪效果还是可以的，但是对于小峰的保留做的不好。而且相对于NASR，SVD要进行大量的矩阵运算，随着采集信号的长度不断增加，会导致矩阵运算量呈现指数倍数的增长，所以一般只会用来处理N<10w的数据。

其他

其他的算法，以后再说。。。。